codetop(21-40)

codetop30——接雨水

42. 接雨水 (opens new window)

就是用一个数组表示一个条形图，问你这个条形图最多能接多少水。

int trap(int[] height);

下面就来由浅入深介绍暴力解法 -> 备忘录解法 -> 双指针解法，在 O(N) 时间 O(1) 空间内解决这个问题。

核心思路（暴力破解）

对于这种问题，我们不要想整体，而应该去想局部；就像动态规划问题处理字符串问题，不要考虑如何处理整个字符串，而是去思考应该如何处理每一个字符。

这么一想，可以发现这道题的思路其实很简单。具体来说，仅仅对于位置 i，能装下多少水呢？

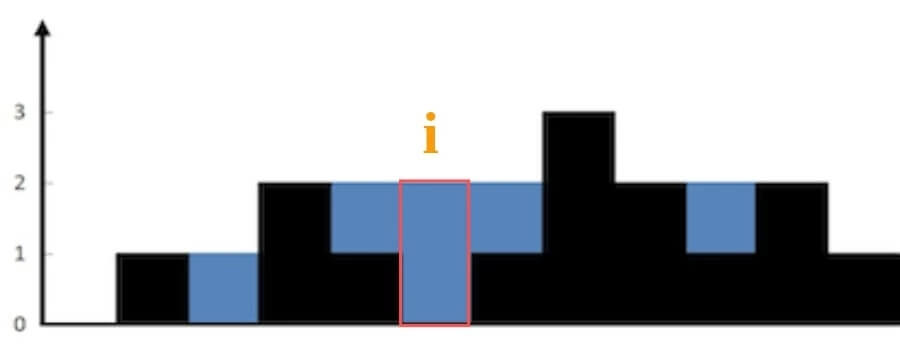
能装 2 格水，因为 height[i] 的高度为 0，而这里最多能盛 2 格水，2-0=2。

为什么位置 i 最多能盛 2 格水呢？因为，位置 i 能达到的水柱高度和其左边的最高柱子、右边的最高柱子有关，我们分别称这两个柱子高度为 lMax 和 rMax；位置 i 最大的水柱高度就是 min(lMax, rMax)。

更进一步，对于位置 i，能够装的水为：

water[i] = min(
               # 左边最高的柱子
               max(height[0..i]),  
               # 右边最高的柱子
               max(height[i..end]) 
            ) - height[i]

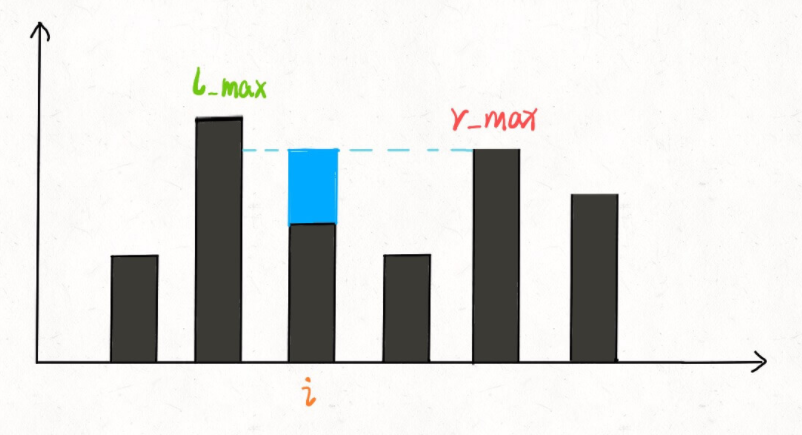
这就是本问题的核心思路，我们可以简单写一个暴力算法：

/**
 * 暴力破解：
 * 1. 分别找到当前位置左边和右边的最大高度
 * 2. 左边和右边最大高度取最小值 - 当前高度 = 当前位置可接的雨水
 * 3. 遍历累加每个位置可接的雨水
 * <p>
 * 时间复杂度 O(N^2)，空间复杂度 O(1)
 */
public int trap1(int[] height) {
    int n = height.length;
    int res = 0;
    for (int i = 1; i < n - 1; i++) {
        int lMax = 0, rMax = 0;
        // 找右边最高的柱子
        for (int j = i; j < n; j++) {
            rMax = Math.max(rMax, height[j]);
        }
        // 找左边最高的柱子
        for (int j = i; j >= 0; j--) {
            lMax = Math.max(lMax, height[j]);
        }
        // 如果自己就是最高的话，
        // l_max == r_max == height[i]
        res += Math.min(lMax, rMax) - height[i];
    }
    return res;
}

这个解法应该是很直接粗暴的，时间复杂度 O(N^2)，空间复杂度 O(1)。但是很明显这种计算 lMax 和 rMax 的方式非常笨拙，一般的优化方法就是备忘录。

备忘录优化

之前的暴力解法，不是在每个位置 i 都要计算 lMax 和 rMax 吗？我们直接把结果都提前计算出来，这时间复杂度不就降下来了嘛。

我们开两个数组 lMax 和 rMax 充当备忘录，lMax[i] 表示位置 i 左边最高的柱子高度，rMax[i] 表示位置 i 右边最高的柱子高度。预先把这两个数组计算好，避免重复计算：

/**
 * 备忘录优化：利用两个数组提前计算 i 位置的，左边最大值和右边最大值
 * <p>
 * 时间复杂度 O(N)，空间复杂度 O(N)
 */
public int trap2(int[] height) {
    if (height.length == 0) {
        return 0;
    }
    int n = height.length;
    int res = 0;
    // 数组充当备忘录
    int[] lMax = new int[n];
    int[] rMax = new int[n];

    // 初始化 base case
    lMax[0] = height[0];
    rMax[n - 1] = height[n - 1];

    // 从左向右计算 l_max
    for (int i = 1; i < n; i++) {
        lMax[i] = Math.max(height[i], lMax[i - 1]);
    }
    // 从右向左计算 r_max
    for (int i = n - 2; i >= 0; i--) {
        rMax[i] = Math.max(height[i], rMax[i + 1]);
    }
    // 计算答案
    for (int i = 1; i < n - 1; i++) {
        res += Math.min(lMax[i], rMax[i]) - height[i];
    }
    return res;
}

这个优化其实和暴力解法思路差不多，就是避免了重复计算，把时间复杂度降低为 O(N)，已经是最优了，但是空间复杂度是 O(N)。下面来看一个精妙一些的解法，能够把空间复杂度降低到 O(1)。

双指针解法

这种解法的思路是完全相同的，但在实现手法上非常巧妙，我们这次也不要用备忘录提前计算了，而是用双指针边走边算，节省下空间复杂度。

/**
 * 双指针：
 * 边走边算，哪边小哪边索引++，只关注左右两边低的柱子
 */
public int trap(int[] height) {
    int left = 0, right = height.length - 1;
    // lMax 是 height[0..left] 中最高柱子的高度，rMax 是 height[right..end] 的最高柱子的高度
    int lMax = 0, rMax = 0;

    int res = 0;
    while (left < right) {
        lMax = Math.max(lMax, height[left]);
        rMax = Math.max(rMax, height[right]);

        /* res += min(l_max, r_max) - height[i]

           l_max 是 left 指针左边的最高柱子，但是 r_max 并不一定是 left 指针右边最高的柱子
           我们只在乎 min(l_max, r_max)，我们已经知道 l_max < r_max 了，至于这个 r_max 是不是右边最大的，不重要。
           重要的是 height[i] 能够装的水只和较低的 l_max 之差有关
         */
        if (lMax < rMax) {
            res += lMax - height[left];
            left++;
        } else {
            res += rMax - height[right];
            right--;
        }
    }
    return res;
}

对于这部分代码，请问 lMax 和 rMax 分别表示什么意义呢？

很容易理解，lMax 是 height[0..left] 中最高柱子的高度，rMax 是 height[right..end] 的最高柱子的高度。

之前的备忘录解法，lMax[i] 和 高度[i] 分别代表 height[0..i] 和 height[i..end] 的最高柱子高度。

res += Math.min(lMax[i], rMax[i]) - height[i];

但是双指针解法中，lMax 和 rMax 代表的是 height[0..left] 和 height[right..end] 的最高柱子高度。比如这段代码：

if (lMax < rMax) {
    res += lMax - height[left];
    left++;
}

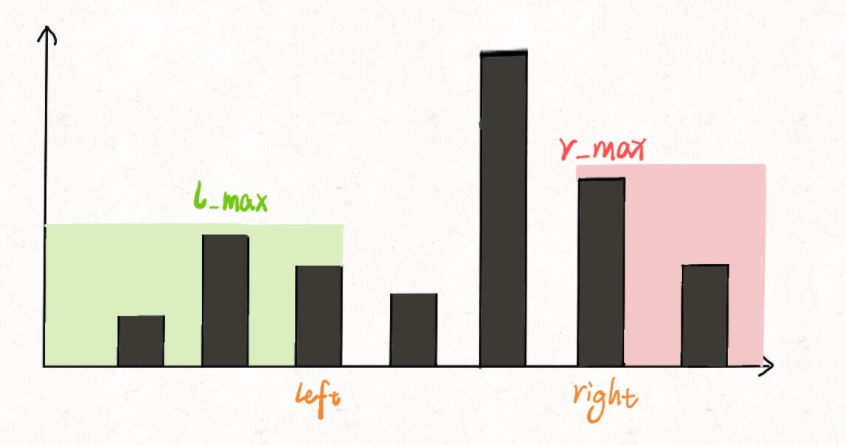
此时的 lMax 是 left 指针左边的最高柱子，但是 rMax 并不一定是 left 指针右边最高的柱子，这真的可以得到正确答案吗？

其实这个问题要这么思考，我们只在乎 min(lMax, rMax)。对于上图的情况，我们已经知道 lMax < rMax 了，至于这个 rMax 是不是右边最大的，不重要。重要的是 height[i] 能够装的水只和较低的 lMax 之差有关：

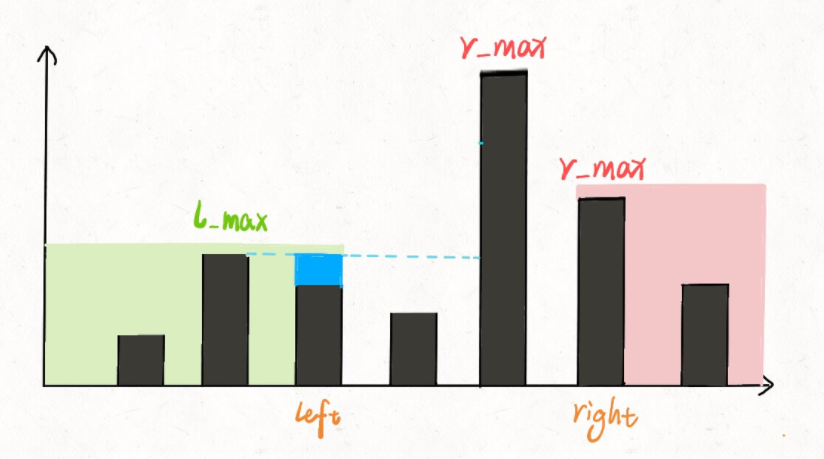
这样，接雨水问题就解决了。

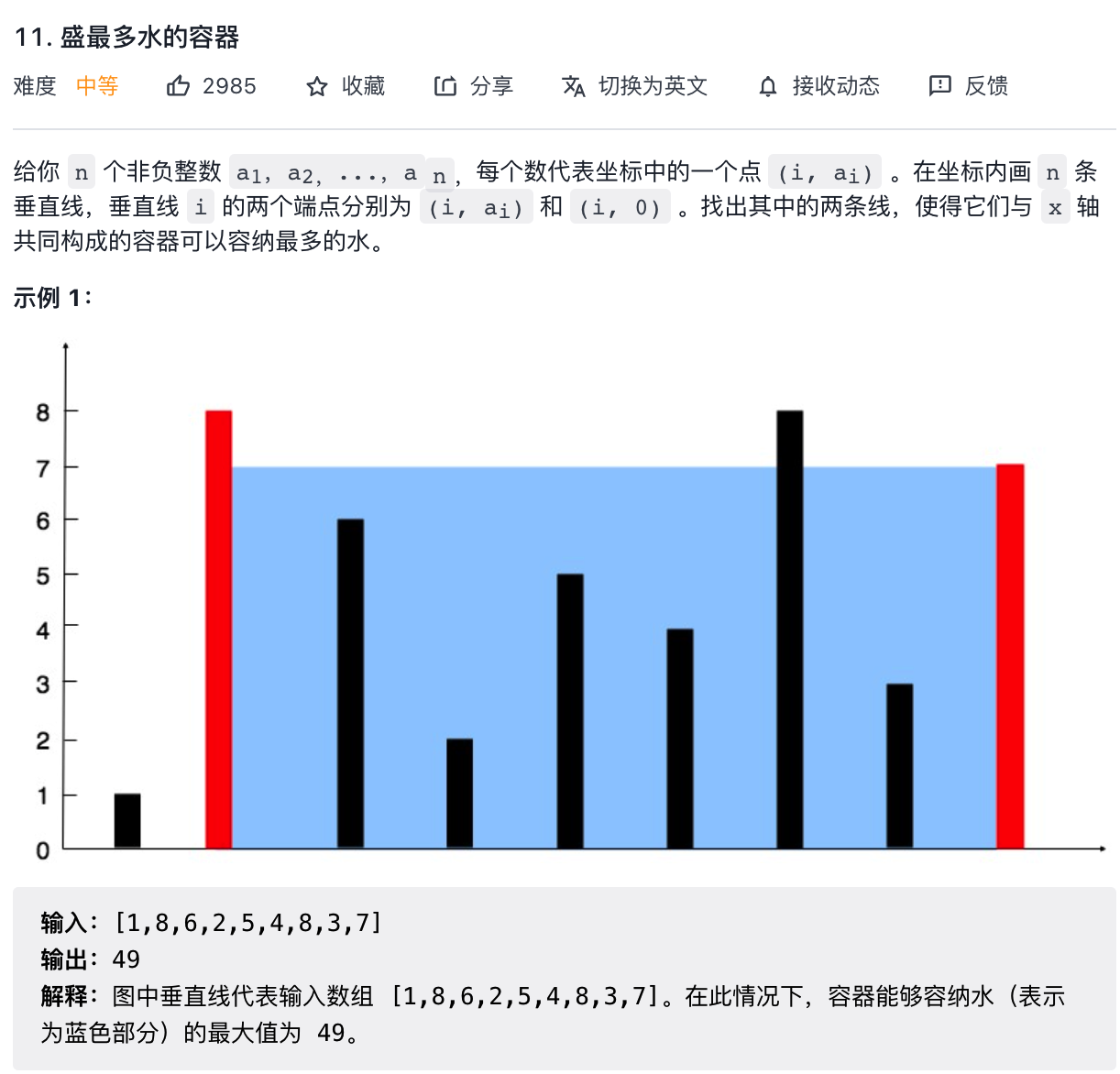
扩展——盛最多水的容器

11. 盛最多水的容器 (opens new window)

这题和接雨水问题很类似，可以完全套用前文的思路，而且还更简单。两道题的区别在于：

接雨水问题给出的类似一幅直方图，每个横坐标都有宽度，而本题给出的每个横坐标是一条竖线，没有宽度。

我们前文讨论了半天 l_max 和 r_max，实际上都是为了计算 height[i] 能够装多少水；而本题中 height[i] 没有了宽度，那自然就好办多了。

举个例子，如果在接雨水问题中，你知道了 height[left] 和 height[right] 的高度，你能算出 left 和 right 之间能够盛下多少水吗？

不能，因为你不知道 left 和 right 之间每个柱子具体能盛多少水，你得通过每个柱子的 l_max 和 r_max 来计算才行。

反过来，就本题而言，你知道了 height[left] 和 height[right] 的高度，能算出 left 和 right 之间能够盛下多少水吗？

可以，因为本题中竖线没有宽度，所以 left 和 right 之间能够盛的水就是：

min(height[left], height[right]) * (right - left)

类似接雨水问题，高度是由 height[left] 和 height[right] 较小的值决定的。

解决这道题的思路依然是双指针技巧：

用 left 和 right 两个指针从两端向中心收缩，一边收缩一边计算 [left, right] 之间的矩形面积，取最大的面积值即是答案。

public int maxArea(int[] height) {
    int left = 0, right = height.length - 1;
    int res = 0;
    while (left < right) {
        // [left, right] 之间的矩形面积
        int curArea = Math.min(height[left], height[right]) * (right - left);
        res = Math.max(res, curArea);
        // 双指针技巧，移动较低的一边
        if (height[left] < height[right]) {
            left++;
        } else {
            right--;
        }
    }
    return res;
}

代码和接雨水问题大致相同，不过肯定有读者会问，下面这段 if 语句为什么要移动较低的一边：

// 双指针技巧，移动较低的一边
if (height[left] < height[right]) {
    left++;
} else {
    right--;
}

其实也好理解，因为矩形的高度是由 min(height[left], height[right]) 即较低的一边决定的：

你如果移动较低的那一边，那条边可能会变高，使得矩形的高度变大，进而就「有可能」使得矩形的面积变大；相反，如果你去移动较高的那一边，矩形的高度是无论如何都不会变大的，所以不可能使矩形的面积变得更大。

codetop33——二叉树的右视图

199. 二叉树的右视图 (opens new window)

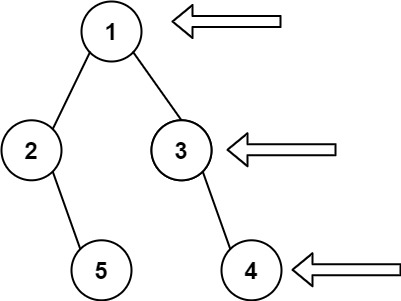
给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

输入: [1,2,3,null,5,null,4] 输出: [1,3,4]

其实问题很简单，就是 [添加每层最右侧的那个节点]。

DFS

此题可以使用 DFS 的方法来解题，因为只需要每层添加 最右侧的节点，所以需要计算层数 depth。

具体代码如下：

List<Integer> res = new ArrayList<>();

/** 记录递归的层数 */
int depth = 0;

/**
 * DFS 解题
 */
public List<Integer> rightSideView(TreeNode root) {
    if (root == null) {
        return res;
    }
    // 前序遍历位置
    depth++;

    if (res.size() < depth) {
        // 这一层还没有记录值，说明 root 就是右侧视图的第一个节点
        res.add(root.val);
    }

    // 注意，这里反过来，先遍历右子树再遍历左子树;这样首先遍历的一定是右侧节点
    rightSideView(root.right);
    rightSideView(root.left);

    // 后序遍历位置
    depth--;

    return res;
}

BFS

利用 BFS 解题，与二叉树的 层序遍历 类似，只是需要先遍历右侧节点，保证队列中先加入的是最右侧的节点。

具体代码如下：

List<Integer> res = new ArrayList<>();

/**
 * BFS 解题
 */
public List<Integer> rightSideViewBFS(TreeNode root) {
    if (root == null) {
        return res;
    }

    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    while (! q.isEmpty()) {
        int size = q.size();
        // 每一层队列中第一个元素就是 最右边的一个元素
        TreeNode last = q.peek();
        for (int i = 0; i < size; i++) {
            TreeNode cur = q.poll();
            if (cur.right != null) {
                q.offer(cur.right);
            }
            if (cur.left != null) {
                q.offer(cur.left);
            }
        }
        res.add(last.val);
    }

    return res;
}

codetop34——重排链表

143. 重排链表 (opens new window)

给定一个单链表 L 的头节点 head ，单链表 L 表示为：

L0 → L1 → … → Ln - 1 → Ln 请将其重新排列后变为：

L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → … 不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

本题实际解题氛围三步—— 【找中点+反转后半部分+合并前后两部分】

public void reorderList(ListNode head) {
    if (head == null) {
        return;
    }
    // 寻找中点
    ListNode mid = middleNode(head);
    ListNode l1 = head;
    ListNode l2 = mid.next;
    // 断开总段后半部分
    mid.next = null;
    // 反转后半段
    l2 = reverseList(l2);
    // 合并链表
    mergeList(l1, l2);
}

/**
 * 寻找链表的中点
 */
private ListNode middleNode(ListNode head) {
    ListNode slow = head;
    ListNode fast = head;
    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    return slow;
}

/**
 * 反转链表
 */
private ListNode reverseList(ListNode head) {
    ListNode prev = null;
    ListNode curr = head;
    while (curr != null) {
        ListNode nextTemp = curr.next;
        curr.next = prev;
        prev = curr;
        curr = nextTemp;
    }
    return prev;
}

/**
 * 合并链表
 */
private void mergeList(ListNode l1, ListNode l2) {
    ListNode l1Tmp;
    ListNode l2Tmp;
    while (l1 != null && l2 != null) {
        l1Tmp = l1.next;
        l2Tmp = l2.next;

        l1.next = l2;
        l1 = l1Tmp;

        l2.next = l1;
        l2 = l2Tmp;
    }
}

codetop35——爬楼梯

70. 爬楼梯 (opens new window)

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

提供四种方法如下：

/**
 * 方法一：
 * 递归解题 （超出时间限制 xxxxx）
 */
public int climbStairs1(int n) {
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }
    return climbStairs1(n - 1) + climbStairs1(n - 2);
}

// 备忘录
int[] memo;

/**
 * 方法二：记忆化 递归
 */
public int climbStairs2(int n) {
    memo = new int[n + 1];
    return dp(n);
}

// 定义：爬到第 n 级台阶的方法个数为 dp(n)
int dp(int n) {
    // base case
    if (n <= 2) {
        return n;
    }
    if (memo[n] > 0) {
        return memo[n];
    }
    // 状态转移方程：
    // 爬到第 n 级台阶的方法个数等于爬到 n - 1 的方法个数和爬到 n - 2 的方法个数之和。
    memo[n] = dp(n - 1) + dp(n - 2);
    return memo[n];
}

/**
 * 方法三：
 * 动态规划解题
 */
public int climbStairs3(int n) {
    if (n == 1) {
        return 1;
    }
    int[] dp = new int[n + 1];

    dp[1] = 1;
    dp[2] = 2;

    for (int i = 3; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    return dp[n];
}

/**
 * 方法四：
 * 动态规划 优化 —— 滚动数组
 */
public int climbStairs(int n) {
    if (n == 1) {
        return 1;
    }
    int first = 1, second = 2;
    for (int i = 3; i <= n; i++) {
        int third = first + second;
        first = second;
        second = third;
    }
    return second;
}

codetop36——二叉树中的最大路径和

124. 二叉树中的最大路径和 (opens new window)

int res = Integer.MIN_VALUE;

public int maxPathSum(TreeNode root) {
    if (root == null) {
        return 0;
    }
    // 计算单边路径和时顺便计算最大路径和
    oneSideMax(root);
    return res;
}

/**
 * 定义：计算从根节点 root 为起点的最大单边路径和
 */
private int oneSideMax(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftMaxSum = Math.max(0, oneSideMax(root.left));
    int rightMaxSum = Math.max(0, oneSideMax(root.right));
    // 后序遍历位置，顺便更新最大路径和
    int pathMaxSum = root.val + leftMaxSum + rightMaxSum;
    res = Math.max(res, pathMaxSum);
    // 实现函数定义，左右子树的最大单边路径和加上根节点的值
    // 就是从根节点 root 为起点的最大单边路径和
    return Math.max(leftMaxSum, rightMaxSum) + root.val;
}

codetop37——区间合并问题

56. 合并区间 (opens new window)

先排序，然后观察规律

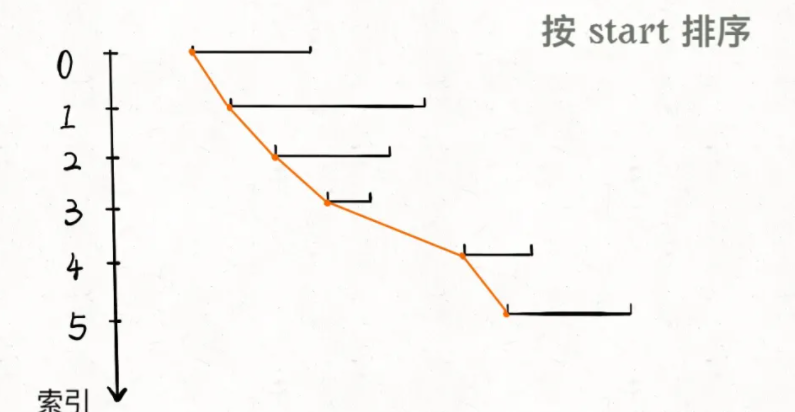
显然，对于几个相交区间合并后的结果区间x，x.start一定是这些相交区间中start最小的，x.end一定是这些相交区间中end最大的。

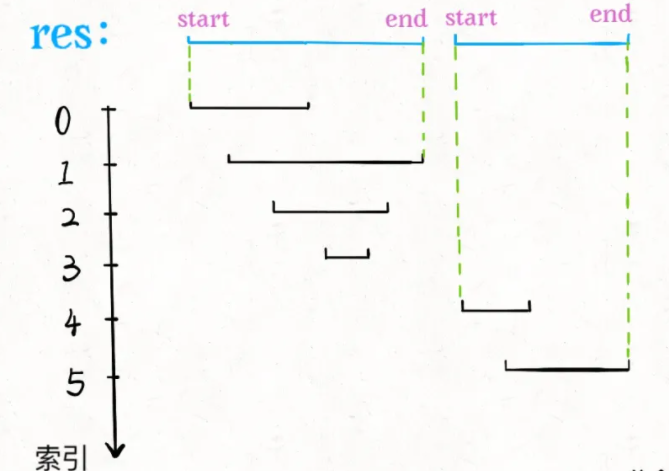
由于已经排了序，x.start很好确定，求x.end也很容易，可以类比在数组中找最大值的过程。

public int[][] merge(int[][] intervals) {
    // 按照 start 对区间进行排序
    Arrays.sort(intervals, Comparator.comparingInt(a -> a[0]));

    LinkedList<int[]> res = new LinkedList<>();
    // 添加第一个方便之后比较
    res.add(intervals[0]);

    for (int i = 1; i < intervals.length; i++) {
        // 当前区间
        int[] curr = intervals[i];
        // res 中最后一个元素的引用（待比较区间）
        int[] last = res.getLast();
        if (curr[0] <= last[1]) {
            // 合并区间
            last[1] = Math.max(last[1], curr[1]);
        } else {
            // 处理下一个待合并区间
            res.add(curr);
        }
    }

    return res.toArray(new int[res.size()][]);
}